Aufgabe 1
Bilden Sie eine Ableitung der Funktion f mit f(x)=x4·sin(3x).
(2 VP)
Aufgabe 2
Lösen Sie die Gleichung (cos(x))2+2cos(x)=0 für
.
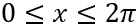(2,5 VP)
Aufgabe 3
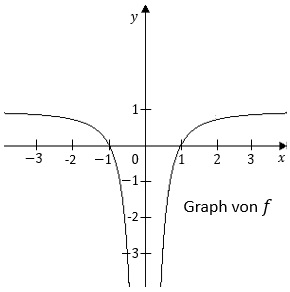Gegeben ist die Funktion f mit 
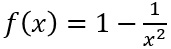, die die Nullstellen x1=-1 und x2=1 hat.
Die Abbildung zeigt den Graphen von f, der symmetrisch bezüglich der y-Achse ist.
Weiterhin ist die Gerade g mit der Gleichung y=-3 gegeben.
a) Zeigen Sie, dass einer der Punkte, in denen g den
Graphen von f schneidet, die x-Koordinate 1/2 hat.
b) Bestimmen Sie rechnerisch den Inhalt der Fläche,
die der Graph von f, die x-Achse und die Gerade g einschließen.
(2,5 VP)
Aufgabe 4
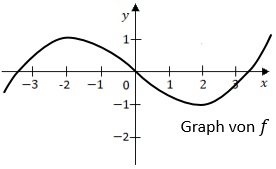Die Abbildung rechts zeigt den Graphen einer Funktion f.a) Einer der folgenden Graphen I, II oder III gehört zur ersten Ableitungsfunktion von f.
Geben Sie diesen Graphen an und begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.
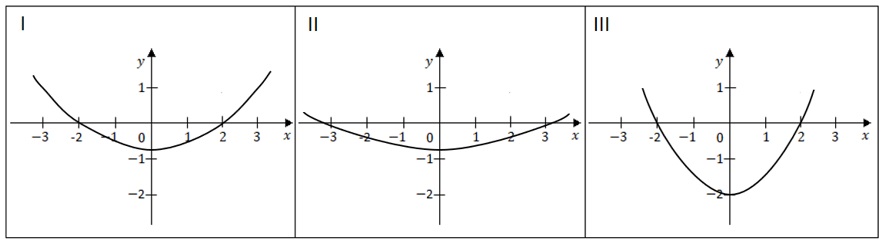
b) Die Funktion F ist eine Stammfunktion von f.
Geben Sie das Monotonieverhalten von F in Intervall [1;3] an.
Begründen Sie Ihre Angabe.
(2,5 VP)
Aufgabe 5
Gegeben sind die Gerade
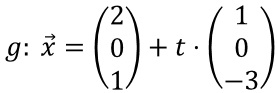und die Ebene E: 3x1-2x2+x3=14. a) Untersuchen Sie die gegenseitige Lage von g und E.
b) Die Gerade h entsteht durch Spiegelung der Geraden g an der Ebene E.
Bestimmen Sie eine Gleichung von h.
(4 VP)
Aufgabe 6
Gegeben ist die Gerade
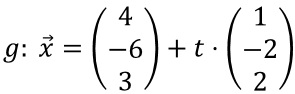. a) Berechnen Sie die Koordinaten des Punktes, in dem g die x2x3-Ebene schneidet.
b) Bestimmen Sie den Abstand des Punktes P(-3|-1|7) von der Geraden g.
(4 VP)
Aufgabe 7
In einer Urne sind eine rote, eine weiße und drei schwarze Kugeln. Es wird so lange ohne Zurücklegen gezogen, bis man eine schwarze Kugel zieht.
Berechnen Sie die Wahrscheinlichkeit der folgenden Ereignisse:
A: "Man zieht genau zwei Kugeln".
B: "Unter den gezogenen Kugeln befindet sich die rote Kugel".
(3 VP)
| Downloads |
PowerPoint